The quantum noise that limits the sensitivity of a detector can have multiple sources. The main contributor is usually the vacuum noise that enters into the interferometer from the dark or also known as the AS (Anti-Symmetric) port.

More generally, vacuum noise will leak into the detector wherever there is an optical loss – which is essentially everywhere! You will see these breakdowns in recent papers such as https://arxiv.org/abs/1807.11734.

There are many, many sources of loss in any given Finesse model, whether that’s some simple loss at a mirror, or some higher order mode loss due to scattering from a surface defect. Finesse uses a multiple-input-single-output modelling method where it introduces vacuum noise at all possible loss points and projects this to a qnoise detector.

It does this multiple noise injection by default, to make your life easier and ensure you as a simulator do not miss a loss source. However, you can also break loss sources down easily using the vacuum command. This plot uses the basic LIGO model from http://www.gwoptics.org/finesse/examples/aligo_sensitivity.php. Below is some code that uses this command to select components separately to inject vacuum noise at to make this breakdown.

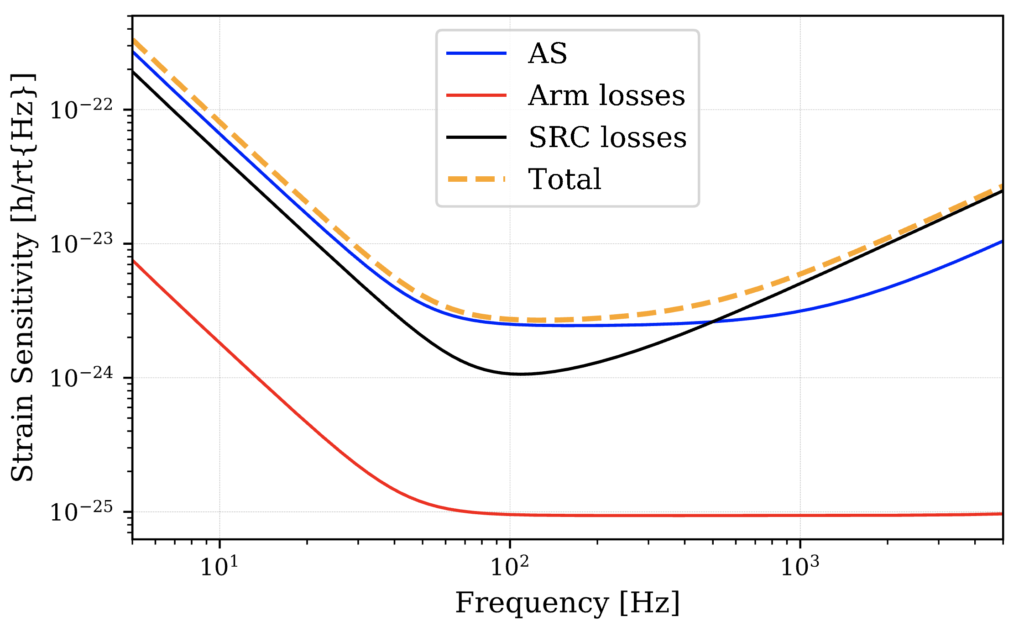
The above assumes a very high level of SRC loss! 10% in fact. This is added to the SRM loss parameter. I have also moved all the loss values from the ITMs to the ETMs, otherwise the ITM contributes towards both the ARM and the SRC loss terms.

The `vacuum` command accepts a list of component names. Any loss or open port at that component will then be included in the quantum noise calculations – `vaccum all` is the default setting.

import pykat
import matplotlib.pyplot as plt
pykat.init_pykat_plotting()

kat = pykat.finesse.kat()
kat.verbose = False
kat.parse("""
l l1 $Pin 0 nin
s s1 0 nin nprc1
# Power recycling mirror
m1 prm $prmT 0 90 nprc1 nprc2
s prc $lprc nprc2 nbsin
# Central beamsplitter
bs bs1 .5 .5 0 45 nbsin n0y n0x nbsout

# X-arm
s ichx $lmichx n0x n1x
m1 itmx $itmT 0 90 n1x n2x
s armx $Larm n2x n3x
m1 etmx 0 80u 89.999875 n3x n4x
attr itmx mass $Mtm zmech sus1
attr etmx mass $Mtm zmech sus1

# Y-arm
s ichy $lmichy n0y n1y
m1 itmy $itmT 0 $michy_phi n1y n2y
s army $Larm n2y n3y
m1 etmy 0 80u 0.000125 n3y n4y
attr itmy mass $Mtm zmech sus1
attr etmy mass $Mtm zmech sus1

# Signal recycling mirror
s src $lsrc nbsout nsrc1
m1 srm $srmT 0.1 $srm_phi nsrc1 nsrc2
s sas 0 nsrc2 nAS

# Force-to-position transfer function for longitudinal
# motions of test masses
tf sus1 1 0 p $mech_fres $mech_Q
const mech_fres 1 # 9 sus-thermal spike
const mech_Q 1M # Guess for suspension Q factor
# DC readout: 100mW = michy_phi 0.07 _or_ darm_phi .00025
const michy_phi 0
const darm_phi .00025

const Larm 3995
const itmT 0.014
const srmT 0.2
const prmT 0.03
const Pin 125
const Mtm 40
const srm_phi -90
const lmichx 4.5
const lmichy 4.45
const lprc 53
const lsrc 50.525

# Differentially modulate the arm lengths
fsig darm armx 1 0
fsig darm2 army 1 180

qnoisedS NSR 1 $fs nsrc2

xaxis darm f log 5 5k 1000
yaxis log abs
""")

_kat = kat.deepcopy()
_kat.parse("vacuum sas")
out = _kat.run()
plt.loglog(out.x, out['NSR'], label='AS')

_kat = kat.deepcopy()
_kat.parse("vacuum itmx itmy etmx etmy")
out = _kat.run()
plt.loglog(out.x, out['NSR'], label='Arm losses')

_kat = kat.deepcopy()
_kat.parse("vacuum srm")
out = _kat.run()
plt.loglog(out.x, out['NSR'], label='SRC losses')

out = kat.run()
plt.loglog(out.x, out['NSR'], label='Total', c='orange', ls='--', lw=2)
plt.legend()