Arbitrary mechanical plants can be specified for each optic by giving a zpk description. The example below makes a simple Fabry-Perot cavity and specifies the longitudinal and pitch plants.

First build the cavity

import numpy as np
from finesse import Model
import finesse.components as fcmp
import finesse.analysis.actions as fact
from finesse.plotting import bode

Pin_W = 5e3    # input power [W]
Ti = 0.014     # ITM transmissivity
Lcav_m = 40e3  # cavity length [m]
Ri_m = 34e3    # ITM radius of curvature [m]
Re_m = 36e3    # ETM radius of curvature [m]

# make the cavity
model = Model()
model.add(fcmp.Mirror('ETM', T=0, L=0, Rc=Re_m))
model.add(fcmp.Mirror('ITM', T=Ti, L=0, Rc=Ri_m))
model.connect(model.ETM.p1, model.ITM.p1, L=Lcav_m)
model.add(fcmp.Cavity('cav', model.ETM.p1.o))

# add input
model.add(fcmp.Laser('Laser', P=Pin_W))
model.connect(model.Laser.p1, model.ITM.p2)

The suspension plants are specified by defining dictionaries with the zpk definition of the plant. The code below defines a simple pendulum plant with a single complex pole. The degrees of freedom which can be read out are z, pitch, or yaw and the degrees of freedom which can be driven are F_z, F_pitch, and F_yaw.

So for example, sus_plant['z', F_z'] is the longitudinal plant in m / N and sus_plant['pitch', 'F_z'] is the cross-coupling of longitudinal motion into pitch in units of rad / N. The code below doesn’t define any cross-couplings.

# define the suspension plant
I_kgm2 = 10  # moment of inertia
M_kg = 0.01  # mass

# for simplicity use the same poles for both pitch and z
F0_Hz = 1  # resonance frequency [Hz]
Q = 100    # Q factor
Fp_Hz = np.array([
    -F0_Hz / (2 * Q) * (1 + 1j * np.sqrt(4 * Q**2 - 1)),
    -F0_Hz / (2 * Q) * (1 - 1j * np.sqrt(4 * Q**2 - 1))
])

# the suspension plant is defined with a dictionary
sus_plant = {}
sus_plant['z', 'F_z'] = ([], 2 * np.pi * Fp_Hz, 1 / M_kg)
sus_plant['pitch', 'F_pitch'] = ([], 2 * np.pi * Fp_Hz, 1 / I_kgm2)
model.add(fcmp.mechanical.SuspensionZPK('ETM_sus', model.ETM.mech, sus_plant))
model.add(fcmp.mechanical.SuspensionZPK('ITM_sus', model.ITM.mech, sus_plant))

Now run the model computing both pitch and longitudinal motion. First compute pitch then detune the cavity by 1 degree so that there is a longitudinal optical spring and calculate the longitudinal motion.

model.modes(maxtem=1)
F_Hz = np.geomspace(0.1, 3e3, 1000)  # the best thing since sliced bread
out = model.run(
    fact.Series(
        fact.FrequencyResponse(
            F_Hz,
            ['ETM.mech.F_pitch', 'ITM.mech.F_pitch'],
            ['ETM.mech.pitch', 'ITM.mech.pitch'],
            name='pitch',
        ),
        fact.Change({'ETM.phi': 1}),
        fact.FrequencyResponse(
            F_Hz,
            ['ETM.mech.F_z', 'ITM.mech.F_z'],
            ['ETM.mech.z', 'ITM.mech.z'],
            name='z',
        ),
    )
)
tfs_pitch = out['pitch'].out  # (1000, 2, 2) matrix of angular transfer functions
tfs_z     = out['z'].out      # (1000, 2, 2) matrix of longitudinal transfer functions

Now plot the torsional spring in the hard/soft basis. The above transfer functions were computed in the ETM/ITM basis. Hard and soft degrees of freedom can also be defined using DegreeOfFreedom and used to compute the transfer functions instead.

gi = 1 - Lcav_m / Ri_m
ge = 1 - Lcav_m / Re_m
r = 2 / ((gi - ge) + np.sqrt((gi - ge)**2 + 4))

hard = dict(ITM=-1, ETM=r)
soft = dict(ITM=r, ETM=1)
vhard = np.array([hard['ETM'], hard['ITM']])
vsoft = np.array([soft['ETM'], soft['ITM']])

# tfs_pitch is in the ETM/ITM basis, so convert to hard/soft
tf_hard = vhard @ tfs_pitch @ vhard.T
tf_soft = vsoft @ tfs_pitch @ vsoft.T

axs = bode(F_Hz, tf_hard, label='Hard')
bode(F_Hz, tf_soft, axs=axs, label='Soft')
bode(F_Hz, tfs_pitch[..., 0, 0], axs=axs, label='ETM')
for ax in axs:
    ax.grid(True, which='major', alpha=0.5)
    ax.grid(True, which='minor', alpha=0.2)
    ax.set_xlim(F_Hz[0], 30)
axs[0].set_ylim(-100, 10)
axs[0].legend()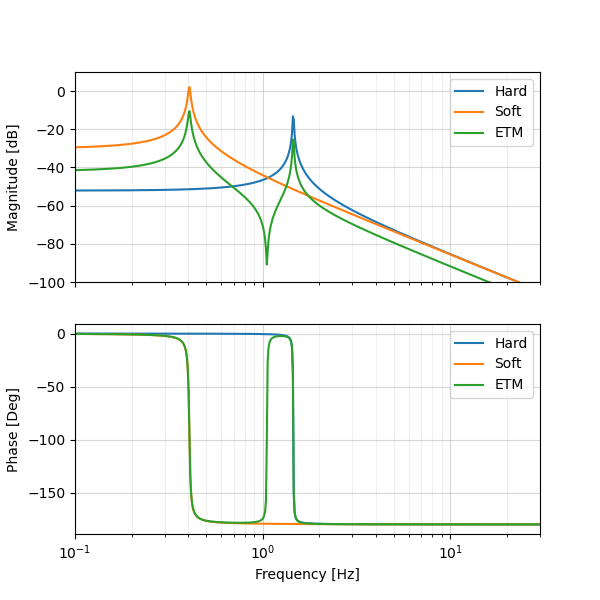

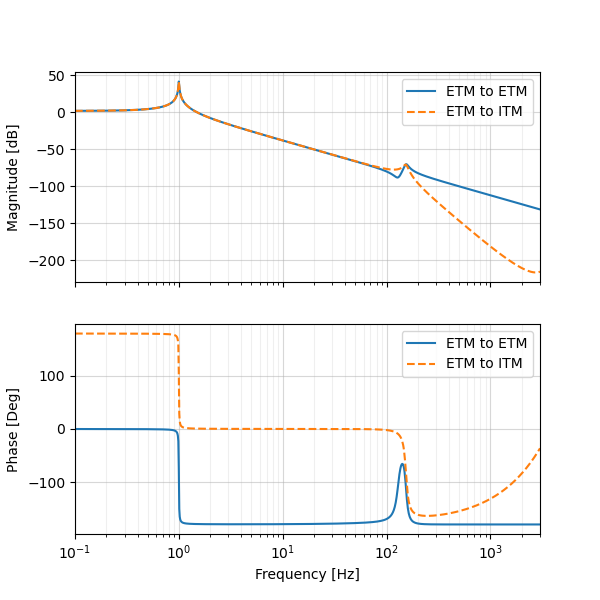
And now plot the longitudinal optical spring.

axs = bode(F_Hz, tfs_z[..., 0, 0], label='ETM to ETM')
bode(F_Hz, tfs_z[..., 1, 0], axs=axs, label='ETM to ITM', ls='--')
for ax in axs:
    ax.grid(True, which='major', alpha=0.5)
    ax.grid(True, which='minor', alpha=0.2)
    ax.set_xlim(F_Hz[0], F_Hz[-1])